Theosophical University Press Online Edition
Part VII - The Dynamic Quantity
Part VIII - The World of Reality
Part IX - The Observer and His Observations
return to Homepage
When we regard the mathematical point, 1l x 1w x 1t, as a basic geometric quantum, let us next consider the possibility of recognizing a corresponding dynamic quantum.
From atomic research we learn that atoms are fundamental to all objects, that these atoms consist of whirling waves of infinitesimal particles, and that neither these particles nor the atoms themselves are permanently connected with any one object, but detach themselves from one body and attach themselves to another, with the result that all bodies are continually subject to change both as to form and contents. This fact points to a distinct relation between geometric and dynamic quantities. This relation was further confirmed when physicists recognized energy and mass to be alike, as mass implies a geometric quantity, and again when evidence was presented showing that both the mass and the form (the dimension in the direction of the moving body) of a body appear to change when its velocity is materially altered.
But the most direct confirmation of the inextricable relation between a geometric and a dynamic quantity is that which we meet with in daily experience, and which shows that any attempt to apply dimensions to the dynamic factors is possible only when these factors are directly related to a body, a geometric quantity. Hence, until any fact to the contrary can be established, we are justified in assuming that these two quantities cannot exist separate and apart from another.
Physical science defines the energy of a body as its capacity to do work, and both energy and work are measured by the product of their weight and the distance through which the weight moves, expressed in either foot-pounds or gram-centimeters. But this convenient method has proved very misleading and has occasioned some strikingly absurd misunderstandings, as was illustrated when the uncontradicted statements of physicists were spread abroad, telling us that action is energy multiplied by time. This was after Einstein had converted clock-time into a geometric dimension and after Planck had introduced a metric constant, known as the quantum of action, and expressed its measurements in gram-centimeter-seconds; and rightly so, for how could a measured quantum of action be other than the measurement of its quantum of energy?
In their effort to formulate their mathematical methods as conveniently as possible, the physicists evidently disregarded the fact that velocity is distance divided by time, v = d/t, and that consequently distance is velocity multiplied by time, d = vt. This shows that space or distance is not a magnitude but a function, the product of two magnitudes, and should be so recognized before we are justified in drawing inferences from physical mathematics.
The terms, time, matter, and space are inappropriate and misleading when applied to the dynamic factors themselves, and as such will be discontinued in this discussion. Henceforth they will be referred to directly as time, weight, and velocity, and considered as three magnitudes and as external representations of dynamic influences or forces universally at work in a nature in which all geometric quantities -- points, planets, and solar systems -- exist in a continuous state of internal activity and external movement. But before assuming that the product of time, weight, and velocity represents the measure of a dynamic quantity, whether that quantity be expressed in terms of action, energy, or work, we must justify such an assumption.
Our earlier references to the importance of distinguishing between a magnitude and a dimension must now be recalled. If time, weight, and velocity are magnitudes, they must be disassociated from the dimensional means by which we measure them. As a magnitude, weight is not pounds any more than velocity is feet, nor must the magnitude time be identified with the seconds ticked off by a clock. Pounds, feet, and seconds are arbitrarily established standards of measurement which, as such, can be applied to the respective dynamic magnitudes for the purpose of obtaining a numerical relativity as a basis for determining a dynamic quantity. But in order to justify this method mathematically, we must show that a condition exists that isolates the numbers from their respective subject of reference and transforms dimensions into numerical relativities. In fact we must be able to establish an inseparable and interdefining relation, between time, weight, and velocity, and in doing so show that these factors represent a community of magnitudes in external nature corresponding to the dynamic community of forces in internal nature.

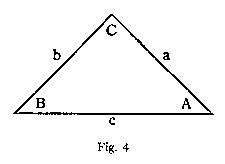
Fig. 4 recalls the isosceles triangle whose three angles represented the functional forces in a dynamic community [see Fig. 1]. Here we shall consider the relation of these forces to their respective magnitudes, as symbolized by the three lines enclosing the triangle, and formulate the following Fig. 4 correspondence:
A -- the initial force B -- the inertial force C -- the directing force
a -- time b -- weight c -- velocity
According to the diagram, weight, b, is a magnitude representing resistance derived from the inertial force, while time, a, is symbolic of an equal and opposite magnitude, representing that which overcomes resistance and as such is derived from the initial force. On the other hand when we regard the lines a, b, and c as subtenses to their opposite angles, B, A, and C, and apply this simile to the magnitudes, the diagram illustrates the fact that all magnitudes are reflections projected into the physical sense-world by their opposite forces. While we shall have opportunity to confirm this statement later, we cannot refer to it without reminding the reader of the following statement by Galileo:
"Philosophy is written in that great book which lies ever before our eyes -- I mean the Universe. But we cannot understand it if we do not first learn the language and grasp the symbols in which it is written. This book is written in the mathematical language, and the symbols are triangles, circles, and other geometric figures, without whose help it is impossible to comprehend a single word of it, without which one wanders in vain through a dark labyrinth."
As we proceed, the significance of this pronouncement will become more and more apparent. Galileo must have realized that for the mind to grasp and visualize a conception of the relation between an inner organic nature and its physical representation in outer nature would seem a hopeless task without the assistance of the geometry of nature.
* * * * * *
When we apply dimensions to the dynamic magnitudes, we learn that the weight of a body can be determined only when that body is free to move, that all moving bodies have velocity, and that velocity can be determined only when this magnitude has been directly related to time. This shows a correspondence between the external dynamic magnitudes and the internal forces. For just as the two equal and opposite forces in the dynamic community are united and coordinated by the directing force, so are weight and time linked together by velocity in the dynamic quantity, as the diagram shows.
Hence experience confirms the inseparable and interdefining relation of weight, velocity, and time, and tells us that a dynamic magnitude, like the geometric magnitude, has no independent existence, and when abstracted from the quantity must include the silent partners that make it an object of thought.
But to complete the correspondence between a dynamic quantity and the dynamic community, experience must confirm that the factors time and weight are magnitudes representing respectively the two equal and opposite initial and inertial forces in an internal action. To do so we must keep in mind that initiative and inertia are linked together in all actions, whether internal or external, and that a dynamic quantity, whether referred to as action, energy, or work, is the product of time, velocity, and weight.
A dynamic quantity = time x velocity x weight.
Let us once more recall the scholium to the Third Law of Motion, from which Newton deduced a metric equivalence between the product of force and its velocity on the one hand, and the product of resistance (weight) and its velocity on the other, and present this equivalence mathematically as follows:
time x velocity x 1w = 1t x velocity x weight.
This presents us with two equal products of only two active factors each, and as the latter product is defined in physics as momentum, we must conclude that the other product represents the two forces that determine momentum. Hence the scholium is not an illustration of the equivalence between an action and its reaction, but between the efforts put forth and the effect accomplished. As these two products have velocity in common (see diagram), we learn from Newton's scholium that time and weight are equal and opposite:
time x 1v x 1w = 1t x 1v x weight.
Let us consider the following dynamic quantities, each representing the product of the time consumed and the velocity and weight of the bodily resistance and measured respectively in seconds s feet f, and pounds p.
1. 2s x 4f x 24p = 192 foot-pound seconds
2. 4s x 4f x 12p = 192 foot-pound seconds
3. 4s x 3f x 16p = 192 foot-pound seconds
These examples present three complete performances of work, all equal in quantity, but different in the quality of work performed. Before considering these quantities in their relation to each other let us determine the rate at which this work was done. To do so we shall reduce each performance to the work done in a unit of time (second).
1. 1s x 4f x 24p = 96 foot-pound seconds
2. 1s x 4f x 12p = 48 foot-pound seconds
3. 1s x 3f x 16p = 48 foot-pound seconds
These corresponding examples of units of work are what in physics is defined as power = work/time. But instead of dividing foot-pounds by seconds, as the physicists do, we obtained this measurement by dividing work by its own number of seconds. Furthermore, according to this interpretation of a dynamic quantity, the product of weight and velocity is not power, but a measurement equivalent to the effort put forth, which in the dynamic quantity is represented by the product of time and velocity. This brings us once more face to face with the question of the relation between time and weight.
As weight differs in the three examples representing units of work, how can time and weight represent two equal and opposite magnitudes? This question was anticipated in Part III, where we presented a synthetic analysis of an internal action and its relation to an external movement, and where we pointed out that the magnitude of the neutralizing initial force is determined by the magnitude of the inertial force (weight). To this we shall add that as we succeed in recognizing the nature of the initial force, we shall realize that this force, when considered by itself, is indivisible, and that therefore a divided time period (the second) serves as a symbolic substitute for the magnitude conditioned by a continually changing resistance. Hence, as the resistance in the work of either man or nature varies according to circumstances, and as work is a totality of units of work, it is in the unit of work that the equivalence between the two opposite magnitudes, time and weight, is established and the value of the second in relation to pounds determined.
This is verified when we examine the three complete performances of work above presented. As the first and second examples maintain the same velocity and represent two equal dynamic quantities, they show that when we decrease the weight we must increase the time consumed in order to accomplish the same amount of work without altering the velocity. This illustrates a rule to which there is no exception, namely, that if we wish to do a certain amount of work in two seconds and maintain a certain velocity, we must overcome twice as much resistance as if we allowed ourselves four seconds for doing so. Hence both experience and the mathematically established dynamic quantity confirm the fact that time and weight stand in an equal and opposite relation to each other.
Let us next compare examples 2 and 3. They are equal in quantity, they consume the same amount of time, and are alike in effort put forth as their measurements of power show. From them we learn that the same amount of power can be maintained by either increasing weight and decreasing velocity or vice versa, but that such changes invariably alter the magnitude of which the time unit (second) is the substitute.
Hence by applying the rules of pure mathematics to the manipulation of the dynamic factors, time, weight, and velocity, we learn that mathematics demonstrates and experience confirms the indissoluble partnership between the dimensions in a dynamic quantity, and establishes a correspondence between this and the partnership between the dimensions in a geometric quantity, and at the same time supports the self-evident recognition of a dynamic community of three functional forces fundamental to action.
While the introduction of the silent partners has nothing to do with mere calculations, as their influence is implied by the usual practice of simply leaving them out, nevertheless it is evidently this practice that helps to explain the failure to recognize the actions behind the working processes of nature. As we proceed we propose to show that the dynamic community represents a major premise from which the science of nature must be developed.
With the aid of the most direct evidence available to man, we pointed out (Part III) that the energy in an organic action is a dynamic community of three functional forces, and that this dynamic community represents the intelligent coordination of the effort put forth and the effect accomplished, and thus unites cause and effect. We have also shown (Part VII) that this direct evidence is confirmed by the mathematical methods employed in physics for measuring the work done by a physical movement, when these methods are in strict accord with the rules of pure mathematics.
Thus it appears that action, energy, and work are three synonymous terms for a dynamic quantity, and that this quantity is the product of three inseparable and interdefining measurements (dynamic factors) abstracted from the magnitudes disclosed by a moving geometric quantity. As all solar and atomic systems are moving geometric quantities, and as both mathematics and experience inform us that initiative and inertia are as inseparably linked together in a dynamic quantity as they are in an organic action, we are justified in thinking that the mathematical methods of physical science, when correctly interpreted, establish a mathematical analogy between the metaphysics of organic action and the physics of a mechanical movement.
This tends to confirm the idea of an intrinsic organic nature in and behind the extrinsic physical nature, and to show that the latter has no reality of its own, but is a self-induced quantitative representation of the former, conveyed to the mind by the senses. Furthermore, because of the limited range of the human senses, physical nature can reveal only what amounts to a mere cross-section of organic nature. If this is correct, it necessarily follows that before an empirical science can interpret the prima facie evidence obtained from physical nature, it must be able to recognize a dynamics which establishes a continuity between the world of appearance and the world of reality.
In Part IV, it was pointed out how direct evidence and experience combine in informing us that an event is the union of an action and its equal and opposite reaction, and that just as such events are fundamental to the mechanical methods constructed by man, so do they constitute a necessary process whereby men sustain and build their own bodies, which in turn appear to us as solidified structures or geometric quantities.
As it is reasonable to assume that there is but one constructive process manifesting itself throughout the whole of nature, the question arises whether the direct evidence, already presented, can aid us to a better understanding of this process. In order to determine this and to test this interpretation by the evidence presented by empirical science, we shall approach the study of nature on the hypothesis that physical nature is a limited sense-representation of an organically constituted, self-acting, self-sustaining, and self-evolving world of reality, and that the latter brings forth all its actions and events by means of a dynamic community or trinity of forces.
* * * * * *
In his work, Where is Science Going? Prof. Planck states that "the utility of a hypothesis, once it has been put forward, can be tested only by following out the logical results that flow from its application." To do so the physicist must place himself in sympathetic mental rapport with the conceptions conveyed by the hypothesis and, for the time being, make them his own, so as to be prepared to reconsider certain ancient propositions which, because of established preconceptions, were completely misunderstood, condemned, and ridiculed, and supposed by the physicist to have been effectively disproved by the application of mechanical theories and physical laws to the operations of nature.
In order to confirm this hypothesis with the aid of the prima facie evidence presented by empirical science, this evidence must be studied in the light of the postulate we have formulated. But before this is possible, this evidence must be divested of the theoretical appendages which have been grafted upon it and with which it has now become identified. All the exact evidence presented has been established by means of mechanical methods, and the theoretical conceptions attached to this evidence are directly applicable to the methods themselves, while their relation to the operations of nature has never been established. Nevertheless it is upon the strength of theory, rather than upon evidence, that physicists have been trying to formulate a mental picture of a universe constructed upon a mechanical pattern.
While it is the intention in future articles to reconsider the evidence on the strength of which Newton formulated his laws of motion and of gravitation, with the view of differentiating between facts and fiction, we find it necessary to prepare the way for this by considering some of the general conceptions and habits of thought which are such a hindrance to any serious consideration of the science of a living universe to which the actions of man can serve as a key.
* * * * * *
One of the first consequences of a hypothetical consideration of a self-acting nature is that we eliminate the usual scientific distinction between an organic and an inorganic nature. In accordance with their presuppositions, Newton and his followers studied a conservative nature existing independent of and yet fundamental to all organic structures. But as the accumulated evidence tends to disprove this, it should have resulted in bringing science into closer rapport with nature.
In fact this dividing line between the organic and the inorganic should have been disposed of when the physicist identified the atom as a structure capable of acting and being acted upon. It should then have been recognized as a self-acting entity in an early state of development. As these atomic entities stand in the same relation to the chemical elements, which are fundamental to the whole of the mineral kingdom, as they do to the different cells in the vegetable, animal, and human kingdoms, we should be able to recognize that the bodies of all these kingdoms are organized hierarchical structures representing more advanced self-acting entities in their march of evolutionary progress.
This conception was further emphasized when the biologists observed that the number of chromosomes in a fertilized egg differentiates the embryos of the various animal forms just as the number of electrons in the atom appears to differentiate one chemical element from another. As soon as we realize that all the kingdoms pertaining to and constituting the earth are bodies of self-acting entities in different stages of development, it becomes evident that while there are both animate (living) and inanimate (dead) bodies, the latter are as organic in structure as the former.
Hence, just as we draw a distinction between a "dead" piece of wood and the "living" tree upon which it grew, so must we draw a similar distinction between an "inanimate" stone and the "animated" rock formation that produced the stone, and between a piece of refined steel and the iron ore which, like a huge plant, grew and spread its branches underground in such soil and locality as can provide the necessary nourishment. When we do this we shall realize that all mechanical methods are conducted with the refined and inert remnants of what were once the bodies of living and growing entities. This should make us realize that any mathematical formulation of such purely mechanical methods from which have been abstracted the intelligence that devised and constructed the methods, can bear no relation to the operations and building processes in a self-acting universe, nor can it serve as a guide to the understanding of them.
We should therefore be able to recognize from the very start that the recorded physical evidence, as formulated and classified by Newtonian physicists, does not support the idea of a self-acting nature. This evidence records what the mind has been trained to observe and was prepared to accept, and nothing else. Nor will the exact measurements so essential to the efficiency of mechanical methods aid science to an understanding of the continuous movements in nature, none of which are automatic or can be duplicated mechanically. The universal characteristic of everything in nature is a distinct difference evidenced by each, and the striking and harmonious uniformity evidenced by all. It is this latter significant and strictly empirical evidence that science has persistently ignored, owing to an inherited disinclination to consider anything but a purely mechanical universe and the supposed laws governing its conservative matter.
We know and can observe that the characteristics possessed by men manifest themselves through action, and that the laws governing individual conduct and that of men's combined and organized efforts are based upon the characteristics exhibited physically by the actions of men. If a correspondence between man and the universe exists, we must determine it by assuming that the laws governing an organically constituted universe, made up of self-acting entities, can be traced back to a principle of action common to them all.
Hence when we attempt to study physical nature as the representation of a self-acting nature, we must not only ascribe distinct characteristics to every entity, but must be able to recognize the necessary dynamic attributes for developing and exhibiting these characteristics through action. And these dynamic attributes must include initiative. In other words, in order to confirm the existence of a self-acting nature we must be able to identify the physical evidence of an initial force and show that cause and effect are as inseparably linked together in nature as the are in the actions of man.
* * * * * *
Scientists recognize that everything in nature is subject to continual change, but they also recognize that in spite of such changes there is something permanent pervading the whole of nature; and that only because of this is it possible to observe definitely these changes and their harmonious relation to each other and to the whole. But not only have they been unable to give us any satisfactory explanation of such changes but, on the general assumption that the building of worlds is an altogether unsolvable problem, they have been confining themselves to reducing nature to a mechanical pattern. This explains their failure to recognize the significant relation between the permanent and the impermanent or transitory, which is distinctly organic (dynamic) and not mechanical, and as such represents the two antagonistic and complementary aspects of life itself.
Some physicists have been comparing the world to a clock that has been wound up once for all, and in support thereof have presented distinct evidence of such a running-down process, while others have been presenting equally competent evidence in direct opposition to this theory. On the other hand, as soon as we recognize every physical event in nature as representing a periodic manifestation of life and therefore subject to birth, growth, death, and decay, this contradictory evidence presents us with a confirmation of an organic nature in and behind the physical.
When in addition to this we take cognizance of the various attempts to calculate the age of the earth and the time of its various progressive changes and also consider the scientific prognostications of the time for the final extinction of the sun, we are justified in wondering why the physicists have never succeeded in recognizing in physical nature the representation of a universal law of periodicity, and why no serious consideration has been given to an energy containing within itself the capacity of building, preserving, and destroying a solar system and everything pertaining thereto.
This was what the ancient philosophers did. They recognized a distinct correspondence between man and nature, they saw in the periodic appearance of men, nations, and races a sequel to the periodic appearance of planets, solar systems, and universes, and they regarded such periodicity as constituting a fundamental process in nature. This process they traced back to a trinity of forces (the dynamic community) as embodying the principle governing the actions of both man and nature.
The reason why they were able to do so was because they recognized a self-acting organic world and understood that its physical representation was conditioned by the more or less imperfect and illusory senses. Hence they concentrated their attention upon the direct evidence of man himself and placed their reliance upon the actual rather than the apparent. By reading our direct evidence into some of the evidence recognized by physical science, we shall, even at the risk of being too precipitate, make a preliminary attempt to show how the relation between the permanent and the impermanent in nature can be traced back to the dynamic community.
But we have another reason for making this preliminary attempt, and this reason was suggested to us by the Kantian philosophy. When in his Critique of Pure Reason, Kant presented his dynamic community, and defined its dynamic relations as inherence, consequence, and composition, he maintained that these relations rested upon the following modes: permanence, coexistence, and succession. The significance of these two sets of definitions will be better understood after we have succeeded in establishing a correspondence between Kant's dynamic relations and the initial, inertial, and directing forces in our dynamic community, as well as a similar correspondence between Kant's modes and the three magnitudes, time, weight, and velocity. But what we wish to call attention to is, that Kant insisted that his dynamic relations together with his modes, are "the analogies and determinators in experience," and as such the means by which to anticipate and interpret experience. It is this pronouncement that we propose to test by applying our graphically formulated postulate, with its forces and magnitudes, directly to recorded experience.

We shall now refer again to the diagrammatic presentation of the dynamic community, Fig. 4, and to the direct evidence of which this diagram is a symbolic description, and consider the two opposite, initial and inertial forces, represented respectively by the angles A and B, and the corresponding magnitudes, time and weight, represented by the two sides a and b. This isosceles triangle, we maintain, gives us a correct description of the relation between the three inseparable forces and their magnitudes, and as such is illustrative of a mathematical principle of relativity fundamental to action, which can be visualized and understood without the aid of exact measurements. To test the truth of this we shall make a preliminary attempt to relate the two opposite forces in the diagram to what is recognized in physics as two independent phenomena, attraction (gravitation) and motion.
In Part VII we pointed out that while the two opposite magnitudes a and b are directly related to their respective forces A and B, these magnitudes are projected into the physical sense-world by their opposing forces. But we also pointed out the necessity of drawing a distinction between magnitude and dimension, and when we do so we shall find that such physical projection applies only to the quantitative or dimensional aspect of these magnitudes and not to the purely qualitative magnitudes themselves.
The reason for emphasizing this distinction will become evident when it is shown how these projections result in an illusory reversing process which, ever since scientists allowed measurements to be their principal guide, has tended to mislead, and has given rise to certain distinct fallacies which are now proving themselves to be the very stumbling blocks facing science today. These fallacies are not readily detected in any mechanical description of nature and are therefore apparently of little or no importance to the applied mechanics with which science has permitted itself to become so closely identified. Yet they have hindered any true understanding of nature's way of working and have served to obstruct the progress of a real science of nature.
* * * * * *
Classical mechanics regarded all physical bodies as consisting of what is called matter, and defined matter as that which can be perceived by the senses or, as that which can be acted upon, or can exert force. To understand this definition let us consider it from the standpoint of the Newtonian physicists themselves, who applied the term matter not only to all bodies but also to one of the three dynamic factors or magnitudes, matter, time, and space, which we have been considering under the terms weight, time, and velocity. The factor matter they measured by standards of weight, pounds or grams, and regarded it as a measure of the force of matter. As these dimensional means themselves were bodies of matter, they identified the force of matter with the pounds or grams, with the result that both matter and the force of matter became considered as quantities.
In formulating a dynamic basis from the direct evidence of man himself, we pointed out the necessity, according to the rules of pure mathematics, of distinguishing between magnitude and dimension, and of recognizing that (1) a magnitude is the physical representation of an organic force, (2) that only the dimensional aspects of the three magnitudes, weight, time, and velocity together constitute a quantity, and (3) that it is these standardized dimensions that establish the numerical relativity between the magnitudes in a definite quantity.
The reason why Newton and later physicists failed to recognize this can be explained only by the fact that the dead and inert remnants with which they conducted their investigations have no initiative of their own, but do possess the opposite force of inertia or resistance. In order to account for this apparently independent force, we shall call attention to the fact that all bodies, animate and inanimate, constitute integral parts of the living and pulsating earth whose initiative is revealed by its ability to call forth out of itself a vast variety of animate structures, to rotate upon its own axis, and to revolve about the sun along a path defined by modern relativists as geodetic, indicating that the earth travels from point to point in a manner which can be considered the line of least resistance.
While Newton regarded inertia as a property inherent in matter, and based his laws of motion upon this conception, we shall assume inertia to be the physical representation of the force of motion. This conception we shall try to justify first by applying it in this test and later by a more searching examination. In this connection it should be noted that the introduction of motion as a force necessitates drawing a distinction between the two terms motion and movement, and of regarding the former as a functional aspect of the latter.
* * * * * *
From physics we learn that weight is continually subject to change, that it alters with every change in the position of the body relative to the earth's center of gravity, and that this change in weight is attributed to the earth's attraction. In succeeding articles we propose to show that attraction is the physical representation of the initial force in nature, but for the purpose of this preliminary test we shall begin by assuming this identity as well as that of the force of motion. But before discussing the relation between weight and attraction, let us consider the relation between time and motion.
As direct evidence, pure mathematics, and the diagram show that the magnitude time, a, is opposite to the continually changing magnitude weight, b, we should expect time to disclose its own inherent and opposite characteristic. The permanency of time becomes evident as soon as we realize that time does not move but that everything moves in time, that it is motion which establishes time periods, and that just as these conditioned and measurable periods reveal time to us, so do they tend to modify our conscious relation to an immovable and permanent time.
As time, the permanent magnitude, is indivisible, science established a divisional time period from the rotation of the earth upon its own axis. This evidence itself is an indication that motion, when considered as an abstract aspect of a continuous movement, is a force which can be directed and which is invariably made to return into itself. This conception was expressed by Platonic rationalists, among whom was Galileo; but this is a subject which will be considered elsewhere.
We have referred to motion as the inertial force, B, and as the diagram shows the magnitude time, a, to be the subtense of the angle B, we find that experience confirms the relation between the organic and the physical by showing how the permanent magnitude time, a, is transformed into a dimension by the impermanent inertial force (motion), as this force reveals these time periods to us. But this does not justify us in attributing the permanent magnitude time to motion.
* * * * * *
From the direct evidence (in Part VII) we learned that the initial and the inertial forces invariably neutralize each other in an action. As these two forces therefore must be equal and opposite, and as the diagram shows that the changeable inertial force, B, (motion), is directly related to the changeable magnitude weight, b, it follows that the initial force A (attraction) must be of a permanent nature, like the permanent magnitude time, a, to which it is directly related. But as it is evidently impossible for an unchangeable and immovable force to alter weight, we must learn how to distinguish between the actual and the apparent by something more certain than formulated measurements which, as the diagram shows, are equally applicable to both of these opposite forces.
When we consider recorded experience in the light of this diagram, we observe how two essentially opposite qualities in organic nature are transformed into quantities in physical nature, that in doing so only the permanent can reveal the impermanent and vice versa, and that these opposites therefore constitute a fundamental necessity in every action. But while we learn how an impermanent force can divide an indivisible magnitude, we shall find that the opposite does not hold good, as it must be evident that a permanent force cannot establish the measurement of an impermanent magnitude.
It is therefore of interest to observe how physicists approach this impossible task. They constructed a cylinder, made from some of the most durable materials, platinum-iridium, whose weight was made equal to that of a liter of water at the temperature of its greatest density (39 degrees Fahrenheit); and this cylinder, which they selected as a standard and permanent measure of weight, they keep protected under the most favorable conditions.
* * * * * *
The dynamic community tells us that it is the inertial force (motion) which alters weight, and that it is the inertial force which is altered whenever the body's position is changed relative to the earth's center of rotation. (The earth has three distinct axes of rotary motion, technically known as axes of inertia, each perpendicular to the others.) It is because any such change of position subjects the body either to an increased velocity and a consequent decrease of inertial force, or vice versa, that weight is altered.
The isosceles triangle shows how any decrease in velocity, symbolized by the magnitude, must be attributed to the directing force, C, and how an increase of this force results in reducing the two opposite forces A and B and in altering the relation between the magnitudes as well. It also shows how the formulated measurements with which physicists support their theory of gravitation are applicable to either one of the two equal and opposite forces.
For the present it may suffice to state that the fall of a body constitutes a physical movement and represents work performed by the earth. Work requires energy and must be supplied by the dynamic community of forces inherent in animate and living bodies only. Hence when the falling apple hit Newton, it revealed to him the representation of an act which cannot be explained away by an immovable, initial force which is a mere abstracted aspect of this fact. As soon as we begin to draw a distinction between a physics applicable to the technically formulated methods of man and a science applicable to the operations of nature, our classical conception concerning gravitation appears to vanish.
* * * * * *
In this preliminary inquiry we have been indicating that both the permanent and the impermanent can be traced back to the two opposing forces in the dynamic community, which according to our hypothesis is fundamental in nature. If this is correct we should expect to find that every antithesis springs from the same source and that the key to a truer conception of the actions and operations of both man and nature is to be found through our ability to recognize these opposites in experience and to understand nature's way of coordinating them. These two questions will henceforth be the subject for our consideration.
In laying the foundation for a method of confirming the postulate of a self-acting, organic world, of which the forms in physical nature are but the sense-representations, concreted shadows, we shall follow in the footsteps of ancient philosophers. Like them we must begin by realizing our kinship and oneness with nature, so as to recognize that all our powers and faculties have come to us from the universe itself by way of the planet to which we belong and of which we are the children.
As no stream rises higher than its source and as no part is greater than the whole, man, with his highly developed powers of ratiocination, should be prepared to concede a corresponding intelligence to a planet, like the earth, with its many differently progressed entities, each constituting a hierarchical structure, like man's own body. In fact we must be able to visualize, as did the ancients, a physical structure like the earth as the physical representation of an organically constituted entity, of which man is the offspring and on which the whole of humanity functions as but one of a series of progressively evolved streams of intelligence, all interacting and all harmoniously interblended.
Life and nature are full of mysteries; but when we awaken to the realization that man himself is an integral part of this mystery, we know intuitively and can discover directly that these mysteries are locked up within ourselves. When we develop all our normal faculties, veil after veil will disappear and we shall be able to penetrate deeper and deeper, and approach nearer and nearer, to the ever-receding and incomprehensible reality itself.
With the X-ray, photography, spectroscopy, etc., together with highly evolved mathematical technique, physicists have extended their investigations into the invisible realms of nature. In this way they have presented evidence of activities beyond man's direct sensory cognition and have disposed of the classical conception concerning "empty space." As these investigations have at times been referred to as metaphysical, we call attention to the fact that this evidence is formulated by the usual quantitative method of physical science, while we propose to consider the qualities fundamental to quantities, with the view of formulating a scientific correspondence between physics and metaphysics.
When we assume that all the processes of nature are interrelated and bound together by one universal principle of relativity, expressing itself in action, it follows that this principle must manifest itself in the simplest as well as the most complex processes in both man and nature. It was upon this understanding that we resorted to a method of identifying this principle by the direct evidence which only man himself can provide.
Recognizing that any direct evidence resting upon intuitive cognition can have no scientific value until confirmed by physical evidence, we selected for our example the act of lifting a bucket of water, and by making deduction and induction complementary, commenced such confirmation by formulating a mathematical correspondence between the dynamic quality in the organic action and the dynamic quantity in the physical action; and presented for consideration the principle of action as a dynamic community of forces and of magnitudes. As a further aid to this we introduced a symbolic geometry for visualizing the relation between a geometrically formulated dynamic quality and its arithmetically formulated dynamic quantity. This geometry, referred to by Galileo as the language in which the philosophy of nature is written, we shall regard as a metaphysical technique which, because fundamental to a physical technique, can serve as a guide and interpreter of the latter.
That two complementary methods are necessary before a scientific interpretation of nature is possible becomes evident when we take into consideration that such interpretation must take into account both the observer and his observations. Our ability to observe is confined to what our training and mental attitude to nature have prepared us to look for and have taught us how to measure and describe. Just as this attitude determines the standpoint from which we study nature, so does it represent the conceptions we entertain of ourselves, our actions, and our relation to nature. The extent, therefore, to which our mental attitude limits our powers of observation and circumscribes the range of our experience is in itself a confirmation of a definite relation between man and nature which, when considered, should make us realize why an understanding of the mind and its functions is a prerequisite to the study and formulation of a science of nature from physical observation.
As soon as man becomes aware of himself as an integral part of the cosmos, he has taken the first step towards the recognition of a correspondence between the forces at work in man and in nature and a similar correspondence between these forces and the functions and faculties of the human mind. As this correspondence becomes understood, we shall know that our interpretation of nature is dependent upon an understanding of ourselves. This was reiterated again and again by ancient philosophers, as for instance by Marcus Aurelius, when he stated:
He who understands not the world order, knows not his own place therein, and he who knows not for what end he exists, understands not himself nor the world.
* * * * * *
During the last century a number of prominent logicians undertook to inform us that "knowledge cannot transcend experience," that the mind cannot reach beyond phenomena, and that however much we may learn about a phenomenal nature, we can learn nothing about the underlying reality. We may investigate as much as we like, we may invent the most delicate instruments with which to lay bare the laws governing the behavior of the most minute as well as the most distant objects accessible to observation, but we shall never succeed in breaking through the charmed circle beyond which alone real knowledge exists.
The general acceptance of such statements by modern scientists and philosophers, known as positivists, resulted in the final and complete break between analytical science and a synthetic philosophy. Kant insisted that before the mind can follow the workings of nature and before the physicist can form a rational conception of her processes, "intuitive cognition must precede experience." However strange this may sound, and however persistently it has been denied by scientists, its truth has been continually confirmed by the very methods employed by modern science.
The scientist, who proceeds by way of hypothesis, deduction, experimentation, and induction, does so in order to formulate his experimental methods and verify the intuitive cognition upon which his hypothesis was based. This scientific practice provides us with evidence showing how the researcher brings something to experience from within himself, which experience itself had not taught him, but had merely been instrumental in calling forth; and which therefore must be confirmed by experience. Whether recognized or not, intuitive cognition has been the essential factor in all the great industrial achievements for which physical science assumes the credit. When intuition, as a necessary function of the human mind, is better understood, physicists will learn how to apply it to the processes of nature as successfully as the inventors have applied it to mechanical methods. Without intuition creative impulse and progress of any kind are impossible.
Every scientist is a more or less conscious philosopher, and his philosophy of life and nature is reflected in the mental preconceptions with which he approaches experience and utilizes his powers of observation. It is his philosophy which establishes his attitude to nature and which qualifies all his attempts to gain knowledge through experience. Just as the mere appearance of an object is determined by the position of the observer, so his conception of this object is determined by his mental attitude towards it.
The physicist who follows in the footsteps of Newton and who confines himself to regarding nature as an assemblage of conservative systems whose configurations were subject to alteration by external agents, of which he himself is one, necessarily observes a very different nature from that described by ancient philosophers who regarded nature as self-acting and, like man, actuated by a governing principle. We can see only what we are prepared to see, everything else is involuntarily shut off and hidden by our own preconceptions. What we learn from experience is determined by what we bring to experience out of ourselves.
* * * * * *
When Copernicus opened the way to a simplified explanation of planetary motions, by identifying the earth as a planet and by stating that all the planets move around a central sun, he presented a conception which was not acquired by experience but by an intuitive recognition which had been called out by the influence of Pythagorean philosophy. Copernicus did not present any heretofore unobserved evidence in support of his conception, but brought the light of a more rational mind to bear upon his observations.
The acceptance of the Copernican system demanded its recognition by the mind as a provisional hypothesis, which could be tested and confirmed only by making objects conform to it, and by making reason follow nature rather than logic. History shows that Copernicus, by an awakened understanding, brought a truth to experience and compelled the mind to translate the evidence of the senses into a simpler and more rational conception of the solar system which, when recognized, became a premise for a new process of logical reasoning.
This bold attempt on the part of Copernicus to reverse men's conceptions of nature struck deep roots. The violent resistance to which it was subjected clearly demonstrated that our mental attitude to nature is not founded primarily upon observations, but upon concepts of a religious and mystical kind. This shows that our attitude to life and nature is usually conditioned by confused concepts representing the conflicting impressions received from two distinct and opposite sources, which we nurse and nourish separately. One of these sources resides in ourselves and, because directly related to the permanent part of being, its impressions are conveyed directly or intuitively to the mind by the inner senses (apperception); while the other source is the continually changing effects of which we acquire knowledge instinctively by way of the outer senses (perception).
This was referred to by Giordano Bruno, whose work on behalf of the Copernican system is seldom referred to and is as little appreciated as is his philosophy of nature. Bruno taught that the conceptual aspect of the mind is a composite of inherent and acquired knowledge and that our intellectual growth is dependent upon our ability to coordinate intuition and instinct. In view of what has taken place since the time of Bruno, it is of interest to note his particular reference to these two kinds of knowledge. He referred to acquired knowledge as methodic and instrumental, and as something which could be made serviceable to higher ends; but he regarded inherent knowledge as the superior of the two, because it contributes directly to the perfecting of the conceptual and reasoning mind. In this way Bruno indicated a distinct relation between the observer and his observation which we shall consider.
* * * * * *
Inherent
and acquired knowledge, like the two opposite forces in an action, are derived from two opposite sources. These two sources should therefore be distinguishable by the characteristic revealed by each of them. When we consider the two opposing magnitudes in the dynamic community as manifesting these characteristics, we may assume the one source to be an all-pervading, permanent, and causal condition and regard the other as the source which makes possible the continually changing and conditioned effects. As it is the physical representation of these two sources we propose to consider in succeeding articles, we shall refer to the one source as the spiritual pole of nature and to the other as the material pole, and regard these two sources as complementary, reciprocal, and necessary to each other.If this is correct, it follows that the same necessity is applicable to the knowledge derived from these two sources. Inherent knowledge, that which makes experience possible, is useful only when related to the material effects to which it is to be applied, and therefore makes acquired knowledge necessary. On the other hand, no amount of acquired knowledge, when considered by itself, will enable us to interpret effects without some complementary inherent knowledge concerning the spiritual cause which makes these effects possible.
Because inherent and acquired knowledge are received by two opposite perceptive functions of the mind, these two functions, like the two kinds of knowledge, must be united and coordinated, and this is the function of the conceptual aspect of the mind. By uniting the intuitive cognitions coming from within with the information gathered instinctively from without, and by coordinating this paradoxical knowledge, the intellectual faculty is developed by the conceptual function, and a balanced judgment is achieved through the art of combining deductive and inductive reasoning. This makes the intellectual faculty the synthetic expression of the complete mind which therefore must be distinguished from the analytical brain-mind that insists upon being guided by acquired knowledge only. With the intellect we must learn to recognize a universally active principle by which cause and effect are combined, and establish its scientific confirmation.
The conceptual mind governs the will, for will is the directing force of the complete mind, whose function it is to coordinate two opposite but inseparable forces expressing themselves as thinking and feeling. These, together with the will, constitute a dynamic community fundamental to an action of the human mind. That the terms thinking and feeling are descriptive of two functional forces of the mind which are complementary, reciprocal, and necessary to each other, will be understood when we realize (1) that our ability to think and to feel is determined by two kinds of knowledge received respectively by way of an inner and outer sense perception, (2) that these two kinds of knowledge are derived from the spiritual and material poles of nature and result in awakening imagination on the one hand and in giving rise to sensation on the other, and (3) that imagination is the permanent characteristic in thinking just as the continually changing sensations are the characteristic in feeling. As man can have no sensation without imagination or vice versa, thinking and feeling are two terms for defining two functional forces in an action of the mind, whose relation to each other corresponds to the relation between the initial and the inertial forces in an action of the organic body.
If our proposition is correct and physical nature is a phenomenal representation of a self-acting organic nature, it should be possible to confirm it scientifically by identifying the representation of these functional forces in the phenomena of nature. But this necessitates that the physicist bring something to experience from within himself, so that he may know what to look for; in other words, the scientific observer must be able to recognize the existence of a fundamental analogy between himself and his observations.
* * * * * *
In this brief resume we have tried to bring out what appears to be the real sum and substance of the functional relations fundamental to the mind, as set forth in the Kantian philosophy. Kant states that "Intuition cannot see and the senses cannot think," and therefore concludes that neither of these is complete in itself, and that because they are derived from two distinct sources (referred to by Kant as time and space) by way of an inner and outer sense, he insisted that the antinomic character of these two kinds of knowledge must be coordinated synthetically before any real understanding is possible.
That Kant's exposition is somewhat involved and obscure may at least to some extent be attributed to the restrictions imposed by the academic conventions of his time. His philosophy has been referred to as pure idealism, which can be justified by the fact that it is largely a synthetic process of deductive reasoning. On the other hand, if Kant's deductive reasoning, which was based upon the direct evidence of the man himself, is correct, it should be possible to test and verify this idealism by applying a corresponding inductive process of reasoning to physical evidence, and in this way obtain from nature some additional and valuable information concerning the very forces working in man.

In preparation for such an attempt we shall record here the correspondence between the different dynamic communities to which reference has been made in this and previous articles. In doing so we shall relate this correspondence to Kant's own dynamic community (see Part VI) whose functional relations he defined as inherence, consonance, and composition and referred to as "the analogies and determinators in experience." In order that we may be able better to visualize these relations we shall refer each of them to the mathematical symbol, Fig. 4, and in addition to this we shall record here the correspondence between Kant's dynamic modes and the physical magnitudes.
DYNAMIC COMMUNITIES
(A -- Inherence) (B -- Consequence) (C -- Composition)
(A -- Initiative) (B -- Inertia) (C -- Direction)
(A -- Thinking) (B -- Feeling) (C -- Willing)
(A -- Inner Percept) (B -- Outer percept) (C -- Concept)
(A -- Intuition) (B -- Instinct) (C -- Intellect)
(A -- Preservative) (B -- Destructive) (C -- Constructive)
MODES AND MAGNITUDES
(a -- Permanence) (b -- Coexistence) (c -- Succession)
(a -- Time) (b -- Weight) (c -- Velocity)