Theosophical University Press Online Edition
Part III - Action
Part IV - Events
Part V - The Mathematical Methods of Physical Science
Part VI - The Geometric Quantity
return to Homepage
What is action? Let us try to answer this question by considering what is involved in the process of producing a movement of the body, so as to obtain some direct understanding of the metaphysical or organic action fundamental to physical movements in general. Whenever I move my body, attempt to lift something or strike a blow with my arm, I know that such movements are caused by an internal energy, and that such energy is necessary to the organic actions of every living entity. In order to determine the nature of this internal energy let us consider the following illustration.
If I wish to lift a bucket of water and place it upon a raised platform, I must ascertain whether I have the power to do so. This I can learn only by taking hold of the bucket, for by so doing I make the bucket of water a part of my bodily resistance. In the attempt to lift the bucket I learn that not only must I be able to overcome my increased bodily resistance, but must have the added strength to move the bucket the required distance. This makes me aware that two distinctly different forces must be brought into play before I can move my body and lift the bucket. One of these is a force whose magnitude must be equal and opposite to the force of resistance and whose function is to neutralize the resistance, while the other is a force whose intensity determines the velocity and direction of the resistance thus neutralized.
The functional difference between these two forces is evidenced by the fact that the magnitude of the neutralizing force is determined by the force of resistance itself, while the intensity of the other force is one of choice, limited only by my organic capacity. This distinction is further emphasized by the fact that any change in velocity alters the force of resistance. Hence it is the necessary function of the one force to maintain the resistance in a neutralized condition, irrespective of its velocity or direction, in order that the other force may be able to perform its function of directing the neutralized resistance. It should therefore be understood that in an organic action the magnitude of one of these forces is predetermined by the resistance itself, while the intensity of the other force is one of intelligent discrimination.
It might be necessary to state here that the reason for introducing the bucket is in order better to illustrate this process of neutralization which, in the actions fundamental to our habitual bodily movement, has become a sort of second nature, and is not so readily apprehended. However, this illustration contains some other valuable hints which will be better understood as we proceed.
The functional difference between these two forces is further verified when I move my arm with the object of striking a blow. Experience has taught me of two distinctly different ways of controlling the impact. I can either place a heavy object in my hand or I can increase the velocity of my arm. In the one case I must increase the magnitude of the force for neutralizing the bodily resistance, and in the other case I must increase the intensity of a force of an altogether different order.
If I now call the resistance the inertial force, the function for neutralizing the resistance the initial force, and the function for governing the direction and velocity of the neutralized resistance the directing force, I can state that an organic action, resulting in a bodily movement, consists in applying an equal and opposite initial force for neutralizing the inertial force, and that when this primary condition is fulfilled, and only as long as it can be sustained, is it possible for the directing force to function and for the organic action to continue.

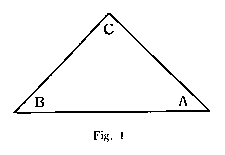
For a better understanding of these dynamic relations let us try to symbolize them geometrically by an isosceles triangle, Fig. 1. This triangle illustrates an organic action, while the angles A, B, and C, represent its three functional aspects respectively, the initial, the inertial and the directing force. Regardless of the particular form or height of this isosceles triangle, the initial and inertial forces always remain equal and opposite, while their joint relation to the directing force is established by the angles themselves, whose sum totals 180 degrees.
It should be evident that the isosceles triangle illustrates an organic action in a manner that words cannot convey, by pointing out how two opposite forces can be united by a third force, capable, so to speak, of embracing them both in the effort to produce an organic action.
This diagram shows also the inseparable relation between the three forces in an organic action, while their characteristic differences should make it evident that none of these forces can function independently of the others. Henceforth we shall adopt a Kantian term intended to convey the same idea, and define the three functional forces in an organic action as a "dynamic community," and regard this community as internal energy. For the purpose of future consideration we shall sum up this evidence as follows:
(a) The internal energy in an organic action is a dynamic community of three functional forces inherent in and fundamental to entitative existence.
(b) Volition and predetermination are inseparably linked together in a dynamic community.
As we propose to consider these functional forces in relation to their corresponding phenomena in nature, it may suffice here to state that when Einstein, in his general theory of relativity, established an equivalence between gravitational and inertial mass and deduced from this equivalence an intensity mass, mathematically defined as a function of velocity, and at the same time declared that "energy and mass are alike," he may be said to have confirmed this threefold division of energy. It should be noted, however, that the real significance of Einstein's division of mass seems to have been lost sight of, as it was so evidently buried in the four dimensional space-time continuum fundamental to his theory.
* * * * * *
When we now begin to consider these internal, organic actions in relation to their corresponding external bodily movements, it becomes evident that the internal actions are metaphysical, dynamic, and qualitative, while the external movements are physical, mechanical, and quantitative. As quantities must be associated with form, the natural inference is that there must be something connected with the qualities that has the capacity to receive form in order that an internal act may be externalized as a physical fact. Furthermore, as experience has shown that a physical fact appears different to different observers, it must be the observer himself who, by virtue of his senses, has the capacity to invest the qualities in organic nature with form, and who by so doing transforms internal acts into external facts, in other words to measurements.
If this inference is correct, I cannot consider my bodily movements separate and apart from my organic actions on the one hand, or from my sense-perceptions on the other, without reducing these movements to mere abstractions. Applying this inference to a constantly moving and changing nature of which man himself is a miniature, I must recognize that the objective reality attached to the forms and movements in physical nature must be attributed to an organic nature in and behind physical nature, and for the purpose of considering the relation between the two, I will postulate that all physical forms are exterior sense-representation of an internal organic nature.
In considering this postulate, we must take into consideration our insufficient knowledge of the human senses, and also their very limited range, of which we but recently have become aware. We know now that the sense of sight can react only to activities taking place in one of the numerous "light octaves" that have been disclosed by spectrum analysis. A similar limitation is revealed by other senses concerning which we know altogether too little. But we know sufficient to realize that all sense-representation is confined to only a small portion of the activities taking place in internal nature, thus leaving the major portion to appear to us as empty space. On the other hand, this very sense limitation enables us to see across this empty space, to extend our vision and obtain a much larger but necessarily illusive picture of a much greater portion of nature. This picture informs us of innumerable heavenly bodies or worlds floating about in empty space, and it was upon this prima-facie evidence that classical physics rested.
As far back as 1881, Prof. J. J. Thomson introduced the idea that mass was of electromagnetic origin. When this was later confirmed, physicists began to recognize that empty space is filled full of electromagnetic activities, whose masses were vastly greater than the mass of any physical body, in fact so much so as to justify Einstein in thinking that the mass of light, because of its great velocity, could be regarded mathematically as infinite. This later evidence therefore tends to confirm the more mature conception of the ancients, who maintained that these floating worlds, apparently separated from one another by a vast empty space, are more closely linked together than are the limbs and organs in the human body.
Some of our scientists have recently been echoing ancient philosophers, like Plato, who insisted that thought precedes nature and that it is the mind that gives shape to the world. Giordano Bruno referred to the physical world as the shadow of ideas, and pointed out that if nature is studied objectively, regardless of its relation to an inner subjective world, it reveals itself as a passive mechanism impelled by blind forces. We observe only how bodies move and how they interfere with one another; and from the determinations based upon such evidence we can learn only how inert bodies and blind forces can be manipulated. Hence, when we allow our conceptions of nature to be guided solely by these observations, we reduce nature to the status of a mechanical automaton. Bruno therefore regarded knowledge based upon observations as negative, and valuable only when considered in its complementary relation to the positive knowledge that must be developed from within, for only with this dual knowledge can experience be properly appraised.
On the assumption that the physical world has a real existence of its own, empirical science has been insisting that our knowledge must conform to objects; but if the evidence presented here is correct, it tends to show that a science of nature must make objects conform to our understanding as it did when it accepted the findings of Copernicus. This was referred to by Kant, who called attention to two sources of knowledge, one of which belongs to the subjective world residing within ourselves, while the other belongs to the objective world existing about us. Kant also pointed out that these two kinds of knowledge, the intuitive and the instinctive must be cultivated by two opposite faculties of the mind, whose relation is analogous to that of the opposite forces in the dynamic community, and as such must be united and coordinated by the intellectual faculty of the human mind.
It is only within ourselves that we can coordinate these two opposite kinds of knowledge and can obtain something more than a mere one-sided concept of the processes of nature. As a case in point, let us consider the relation between cause and effect usually recognized as successive, every cause producing an effect which in turn becomes a cause, and so forth. But as soon as we recognize the efforts put forth as the cause, my own actions as already indicated, inform me that the effort put forth cannot function apart from the effect accomplished and that cause and effect are inseparably linked together in the dynamic community.
When I recognize physical facts as the external representation of internal acts, and on the strength of this refer to internal nature as the causal world and to external nature as the world of effect, and at the same time recognize the efforts put forth as the cause, I am faced with a paradox that the effect must be present in the cause, and furthermore that the cause must reside in the effect. If this is correct, this cause and its relation to the effect should be recognizable in every physical fact. That modern science has not recognized this only goes to show that an understanding of nature cannot be acquired either by observation, measurements, or mathematics unless the physicist has something from within to bring to bear upon experience. Before we can find anything we must know what we are looking for.
The same idea was expressed somewhat differently by Kant when he stated that "no mere observation, no accidental association of sense-impressions and ideas, however thorough these may be, will enable us to become aware of a self-evident, necessary and universal truth." He said also: "We may analyse as much as we like, we shall never arrive from one object and its existence at the existence of another, or at its mode of existence by means of the concepts of these things only." And again: "Suppose we should carry our empirical intuition even to the very highest degree of clearness, we should not thereby advance one step nearer to the knowledge of the constitution of objects."
As we proceed we expect to show that these pronouncements were not those of a biased mind, but of a constructive critic and intuitive philosopher, whose aim was to enhance the value of an empirical and analytical science by calling attention to the importance of a complementary synthetic science and by emphasizing the necessity of studying nature deductively from within as well as inductively from without. But of the two methods he regarded the former as the more important, just as he insisted that the conviction arising from a knowledge of oneself constitutes the final "court of appeal." Kant's position was akin to that of Giordano Bruno, who demanded that we make the evidence of the senses conform to a rationalistic, reasoning process which must be guided by our innermost convictions.
As experience has shown that we can see only what we are prepared to see, it necessarily follows that in order to establish a physical confirmation of the dynamic community, we must approach nature as did the ancient philosophers, who made man's knowledge of himself paramount and who regarded nature, like man, as a bipolar entity, from whose inner pole emanates a life-giving spiritual essence that pervades the whole of nature and makes possible every effort put forth; and from whose outer pole streams forth the life-receiving material essence upon which such efforts may be exerted, while it is the mysterious power inherent in the entity itself that unites these two essences and transforms them into a dynamic community. (Internal Energy)
It is the antinomic relation between the two poles of nature that gives rise to the paradoxes with which true philosophy abounds. Instead of regarding them as contradictions to be avoided, science should welcome them as valuable guides to an understanding of nature. When we succeed in harmonizing the inner experiences recorded by the great mystics of every age with the facts presented by the great physicists of modern times, philosophic romancing will be supplanted by a conviction strong enough to recognize in the active union of the spiritual and material aspects of nature the keys to a scientific confirmation and a mathematical formulation of a self-acting, self-contained, and self-creative nature.
The very first of these keys is this dynamic community. Before considering this key itself, I wish to point out how this community of forces together with the principles of causation becomes fundamental to what in the Kantian philosophy was defined as "synthetic unity."
My concept of a trinity of forces representing a dynamic community fundamental to action was derived from two sources of knowledge, and is the result of combining inherent and acquired knowledge. The inherent or intuitive knowledge was called into activity by my interest in and study of ancient philosophy, while the acquired knowledge was gained through practical experience as a mechanical engineer. Hence, this concept combines a synthetic deduction from ancient philosophy and the application of a corresponding method of induction to the facts of nature, and as such meets the requirements for a rationalistic as well as a logical intellectual concept, according to both Galileo and Kant.
This trinity and its fundamental relation to nature can be found recorded in the Vedanta philosophy, in the Book of the Dead, in the Kabala, in the symbolic language of the Old and New Testament, in the writings of Plato and other Pythagoreans, and in many other ancient systems of thought, when we learn how to recognize it. It was first brought to the general attention of the Christian world through the heroic efforts of Giordano Bruno. Later, certain aspects of Bruno's philosophy were elaborated upon and formulated more cautiously by other philosophers, and we can recognize this principle in Spinoza's "Substance," in the "Monad" of Leibniz, and in the "dynamic community" which, according to Kant, is basic to synthetic unity.
However, it must be distinctly understood that the recognition of one identical metaphysical trinity fundamental to the many different ancient symbolic expositions as well as to a number of modern philosophies, would not have been possible without the aid received from the profound writings of H. P. Blavatsky, who in The Secret Doctrine expounds this trinity in its purely metaphysical aspect, and presents it as the first fundamental proposition in the teachings of an archaic philosophy. According to this ancient wisdom-teaching, reasoning man has lived upon this earth some eighteen million years, and has occupied different faces of its continually changing surface. The universal recognition of these truths, like the rise and fall of civilizations, is one of "cyclic recurrence" which, during the Christian era and until this work was published, had become an altogether "secret doctrine."
In order to verify these statements, H. P. Blavatsky presented a number of keys to the understanding of the esoteric language in which this archaic teaching had been recorded in ancient manuscripts. With the aid of these keys she traced the archaic philosophy through a series of ancient and modern religions, philosophies, and sciences, and pointed out how its teachings had become subjected to different literal interpretations and distortions, and finally had been completely lost sight of. But it should be borne in mind that these keys and the teachings that they reveal must be judged entirely upon their merit and not upon the authority of anybody's "say so." When this work -- The Secret Doctrine -- was first published in 1888, the Western world evinced but little interest in ancient civilizations or in pagan literature. Since then much more authentic information concerning these has been gathered and has given more and more astonishing glimpses into the great past. When once we begin to realize how closely humanity's future is linked up with and is foreshadowed by its past, we shall no longer fail to take into account the complete isolation from this great past to which the Western world was violently subjected by a zealous Church. It was this isolation that paved the way for the Dark Age, while only the last few centuries represent a period of gradual reawakening, during which the struggle between the forces of light and darkness, progress and retardation, is becoming more and more accentuated.
* * * * * *
Ancient knowledge was formulated by a mentality very different from ours, just as the ancient attitude to nature is altogether foreign to us. Yet the universality of the archaic teachings points to a great antiquity, while their mature outlook upon life and nature makes it evident that they have been tested by ages of experience and have persisted from one period of enlightenment to another. To reclaim the truth contained in "the wisdom of the ages" requires an open mind and an earnest effort to interpret its profound thought-pictures so as to be able to express them in terms suitable to our own mental development and to make them helpful in meeting the many problems facing humanity today.
In doing so we shall be able to recognize the marked contrast between ancient philosophy and modern physical science, whose fleeting theories have been resting largely upon a dualistic attitude to nature. This attitude became conventionally established in the Western world when the writings of Aristotle were interpreted by the early scholastics in such a way as to provide a suitable metaphysical support for dogmatically formulated theology. This metaphysics postulated a complete separation between the two poles of nature, which according to the ancients are as inseparably linked together as are the poles of a magnet.
The scholastic interpretation was later strengthened and was able to assume a recognized position in modern philosophy when Descartes introduced a Cartesian dualism postulating two distinct worlds, one of spirit and one of matter, and each endowed with a homogeneous substance of its own. This complete refutation of the philosophy of Bruno, Kepler, and Galileo opened the door to an independent investigation into the world of matter, without coming into direct conflict with a theology supposed to be applicable only to the world of spirit.
It is therefore of interest to note that the year 1642 not only closed the stormy career of Galileo but also gave birth to Isaac Newton, a more practical and mathematical genius who, on the strength of this Cartesian dualism, was able to disarm opposition and sweep aside the many obstacles confronting Galileo. Unlike Galileo who, because of his intuitive understanding of nature, resorted to experimental methods for purposes of illustration and verification, Newton based his knowledge upon the methods themselves and his philosophy of nature constitutes a process of induction from these very methods. He attributed the fall of the apple to a universal force, gravitation, maintained that inertia was a property with which God had endowed homogeneous matter, and on the whole introduced conceptions that the minds of the men of his time were prepared to accept. When he formulated his laws of motion, he laid the foundation for an empirical science that has proved itself an invaluable aid in this age of invention.
The real value of Newton's work must be appraised in the light of his time, and whatever the future estimate may be, it speaks for itself as a necessary and important stepping-stone to the real science of nature, which so evidently was the one and only aim of Newton himself.
* * * * * *
Side by side with the painstaking efforts made by analytical physicists to formulate a world-picture with the aid of measurements and mathematics, we must consider the series of similar attempts made by the synthetic philosophers already referred to, whose conceptions of nature were based upon self-examination, reflection, and inner conviction. But none of these philosophers succeeded in relating his world-pictures to experience, that is, to experience as formulated and presented to us by the mathematical physicists. We have already mentioned the unsuccessful attempt made to apply Kant's synthesis to physics which, a century ago, resulted in completing the break between philosophy and science. This failure may be said to have been anticipated by Kant himself, for the reason is explained by him in one of his latest utterances (printed as a footnote in his Critique of Judgment):
It has been thought a doubtful point that my division in pure philosophy should always be threefold. But that lies in the nature of things. If there is to be an a priori division it must be either analytical, according to the law of contradiction which is always twofold, or it is synthetic. And if in this latter case it is to be derived from an a priori concept, the division must necessarily be trichotomy. For according to what is requisite for synthetic unity in general there must be (1) a condition, (2) the conditioned, and (3) the concept which arises from the union of the conditioned with the condition.
A philosophy of nature whose method of deduction is synthetic or threefold cannot be expected to be in agreement with, or substantiated by, an empirical science whose method of induction is analytical and twofold; particularly when these two methods are based upon entirely different premises. The synthetic philosopher maintains that cause and effect are inseparably linked together in nature, while Newton and the Newtonian physicists regard cause and effect as belonging to two distinctly separate compartments of nature.
As an example of this essential difference, let us consider Newton's third law of motion: "To every action there is an equal and opposite reaction." His law has proved itself a valuable contribution to a science whose knowledge was confined to information obtainable from mechanical methods and whose object was largely to construct more and more effective mechanical devices; and while this equivalence is incontrovertible, it is nevertheless an incomplete and misleading statement when considered as a description of nature's way of working. How could anything happen in a nature in which action and reaction did nothing but neutralize and cancel each other? Certain it is that his equivalence is a poor guide to the understanding of a nature where everything is subject to continuous changes resulting in either growth or decay.
* * * * * *
Let us consider the following scholium to the Third Law of Motion, from which Newton abstracted this equivalence.
If the action of the external agent is estimated by the product of its force into its velocity, and the reaction of the resistance in the same way by the product of the velocity of each part of the system into the resisting force arising from friction, cohesion, weight, and acceleration, the action and reaction will be equal to each other, whatever be the nature and motion of the system.
According to Newton man was an external agent, endowed with powers to act that were beyond human understanding. Hence self-acting man was distinguished from the conservative systems of which the physical world was supposed to exist. In order to determine the action of this external agent he established a metric equivalence between this action and the product of the resistance of the system and the speed of its motion. When later physicists substituted the term energy for the action of the external agent, and the term work for the corresponding reaction, and established an equivalence between energy and work, this equivalence was made the basis of the doctrine of the conservation of energy, for according to such eminent authorities as Lord Kelvin and Clerk Maxwell, nearly the whole of this doctrine is contained in Newton's scholium quoted above.
The textbooks in physics of today tell us that "the energy of a body is its capacity to do work," that work is measured by the product of the weight of the body and the distance through which it moves, and in addition to this they volunteer the information that "in physics the word work is used to describe not the effort put forth but the effect accomplished." This seems to show that the physicists have failed to recognize the significant fact that when I wish to change the position of a bucket of water, I must for the time being make that bucket an integral part of my own internal energy, and that the same is true when, instead of my own energy, I substitute the energy of a steam engine or an electric motor.
Experience shows that initiative and inertia -- representing two opposite forces expressing themselves through appropriate media -- must be linked together in all the movements in physical nature and in every kind of mechanical work produced by man. However, there is a very essential difference between the work of man and the work of a steam engine. For while the reaction to the work of man tends largely to strengthen and sustain him, the reaction to the work of an engine tends only to wear it out and destroy it.
But irrespective of this difference, when, instead of studying facts analytically, we consider them synthetically, we learn that every action and its equal and opposite reaction combine to produce a transformation. When we now apply the term "event" to such transformation it is clear that an event is the union of an action and its equal and opposite reaction.
This definition completes Newton's analytically formulated equivalence, and establishes an event as the manifestation of what Kant called synthetic unity, namely, the concept which arises from the union of the conditioned with the condition, in other words, the union of the reaction with the action.
According to Kant synthetic unity constitutes an "apodictic verity," in other words, something basically evident, whose recognition he regarded as necessary to an understanding of the processes of the mind and the processes of nature. It is the object of this series of articles to confirm this, and to show that the Kantian synthesis is fundamental to each and every operation and structural formation in a constantly changing nature, and that the growth and decay resulting from such changes are the eternal co-workers with birth and death in that continuity of life which we know as nature.
* * * * * *
Physicists have presented us with a multitude of analytically formulated methods that enable us to manipulate and mold material external to ourselves, but they have failed to consider the synthetic process fundamental to these methods by means of which man and other entities sustain themselves and mold the material of their own bodies. Let us consider mechanical methods in the light of a dynamic process.
Every mechanical method originated in an attempt to reduce an idea to practice. This makes a method the physical manifestation of a concept in the mind of the inventor. Every experimenter knows, if he stops to think, that his success depends upon his ability to construct a device whose actions and reactions unite in producing results -- events -- corresponding to the concept in his mind. But owing to their conventional attitude to nature, physicists have been in the habit of ABSTRACTING FROM THE METHODS THE VERY MIND THAT CONCEIVED AND CONSTRUCTED THE METHOD, just as Newton abstracted an equivalence from an event and established this isolated equivalence as "a law of motion." Herein lay the seed of materialistic science. This method of abstraction was referred to by Kant when he said: "As soon as we abstract in thought our own subjective nature, the object with the property ascribed to it disappears, for it is the subjective nature that determines the form of the objects as phenomena."
A concept is energy, a dynamic community, and it is constructive because one of its functions is the directing force of intelligence (volition) that manifests itself in the methods of man as it does in the processes of nature. But owing to their habit of abstraction and analytical formulations, physicists are unable to recognize its manifestation in physical nature. The attempt to abstract this force from the processes of nature explains why analytically formulated methods are debarred from serving as guides to an understanding of nature.
It is with the directing force of intelligence that man creates his environment and, like nature, molds his exterior form. The present intense activity of this force accounts for the inventions and industrial achievements of recent times, while the failure to recognize its directing intelligence and to understand its real nature and influence in the life of humanity explains the present worldwide disturbances -- both mental and economic.
It is therefore a hopeful sign that the more progressive scientists are now recognizing that their pronouncements are incomplete and unsatisfactory, and that whether they know it or not, it is the manifestation of the directing force of intelligence that Einstein, in an involved and roundabout way, has been trying to formulate mathematically and introduce into physics as "intensity mass."
As we proceed I expect to show that a rational and intellectual conception of the processes of nature must be evolved from a philosophy that has its source in the knowledge of the complete being of man, while the function of empirical science is to test, reject, or confirm the concepts of man. Empiricism, by itself, cannot establish a firm conviction in the mind.
When we regard man as a child and an integral part of nature, instead of an external agent, it is evident that only in ourselves can we unite an inner and outer percept into an intellectual concept, and learn to understand something about the dynamic processes governing nature which, like man, is self-acting; while the scientific recognition of such a concept is necessarily dependent upon the ability to confirm it empirically.
* * * * * *
When we apply the synthetic method of induction to Newton's above-quoted scholium, we find that the event arising from "the union of a reaction with its action" is a transformation in the body of the external agent himself, and that no such internal transformation is possible without a corresponding external movement. It is this external movement that physicists abstracted from the constructive process of nature, and defined as work, and formulated mathematically as the product of weight and distance.
Newton determined the action of the external agent by measuring the reaction manifesting itself in the alteration of the system to which the action was applied, as for instance that of lifting a bucket of water onto a raised platform. Let us consider this reaction. As the bucket is placed upon the platform, the platform reacts to the impact of the bucket, thereby producing another event whose action constituted the reaction in the previous event, while the reaction of the platform to the impact may occasion several simultaneous events whose combined reactions must be equal to the impact. Each of the reactions of these simultaneous events in turn will give rise to succeeding events and so forth ad infinitum. As an endless series of events cannot possibly have a beginning, it necessarily follows that, just as every reaction becomes an action in a succeeding event, so every action originated as a reaction in some previous event. From this we learn that every event in nature is the effect of an endless succession of events and the cause of other endless successions of events.
I have defined my bodily movements as physical representations of actions of my organic body; and realizing that all such voluntary actions originate as reactions to corresponding actions of my mind, I obtain the idea of a continuous interaction between the mind (the condition) and the body (the conditioned) through which the mind expresses itself, and learn that the union of these actions and reactions results in a series of transformations (events) that are as essential to the growth and well-being of my mind as they are to the body. In other words, this interaction constitutes a necessary process for improving my mind and developing my body and sustaining my existence as a self-acting entity.
When once imbued with the idea that the processes of nature are universal and intelligently directed from within, self-conscious man is justified in basing his general understanding of these processes upon the self-evident knowledge of his own being. This being done, the conviction will force itself upon his mind that the interaction between mind and body is indicative of a constructive process that is repeating itself all through nature, and is actually confirmed by the constructive methods of man, as has already been pointed out. When we recognize that the event, manifesting itself as the physical form of man, is the consummation of countless events, we must recognize also that a similar constructive process is fundamental to the manifestation of every other form in nature and that the whole of nature is an event, the consummation and manifestation of a totality of past events.
* * * * * *
Physicists have been studying the interference to which these events are and can be subjected, and by their method of isolation have gathered a mass of metric evidence based largely upon a destructive process, and it is the theories formulated from this evidence that have been applied to the methods of man. As these theories are analytical formulations and as such conceal the directing force of intelligence, they have resulted in keeping physicists and laymen alike from recognizing the constructive process in nature, which is universal and synthetic. But when physicists are prepared to approach their studies with the conception that universal nature is a natural unfoldment from within and the representation of a totality of events, they will recognize that in the harmonious grouping and correlation of events is mirrored forth an intelligently directed and constructive process, and that the key to the understanding of this process is to be found in the constitution of the event itself.
This was significantly indicated by Jacob Boehme, the uneducated shoemaker and mystic of the sixteenth century, when he stated that "multiplicity cannot be derived from unity" (as generally understood), and that therefore "the great diversity necessitated a multiplicity within the fundamental unit from which all proceeds."
As we proceed an attempt will be made to confirm this profound statement by showing how the physical phenomena, revealing themselves in the great diversity of nature, are explainable only when considered in the light of the dynamic community, fundamental to synthetic unity. This was recognized by Kant who referred to the functions in the dynamic community as "the analogies and determinators in experience."
* * * * * *
I have defined an organic action as a dynamic community, and have symbolized it geometrically by the angles in an isosceles triangle (Fig. 1). When we recognize that this organic action originated as a reaction to an equal and opposite action of the mind, and define the union of this action and reaction as synthetic unity (event), we can also present a geometric diagram of synthetic unity, with the aid of some very ancient symbols.
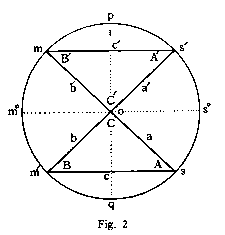
Fig. 2 is adapted from what is known as "the (decussated) cross in the circle." By joining the two upper and the two lower ends of this cross, I transform the cross into two equal and opposite isosceles triangles. The content of the lower upright triangle represents the action of the mind, while its reaction is similarly represented by the inverted, upper triangle, corresponding to the organic action symbolized in Fig. 1 by an upright triangle. The circumference enclosing the two triangles is symbolic of the event resulting from the union of an action and its reaction. This is indicated geometrically by the angles of the two triangles whose sum totals the 360 degrees contained in the circumference.
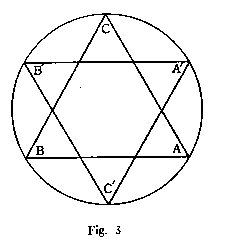
Fig. 3 is another ancient symbol known as "the interlaced triangles." It gives us another and more graphic description of the interaction and its result, as the interlacing of the triangles results in producing a hexagon whose angles together with the angles of the two triangles total 3 x 360 degrees. This makes the circumference represent the contour of a three dimensional concrete form, a sphere or spheroid.
As we shall have occasion to consider these diagrams more fully as we proceed, I will only point out that just as the dynamic community combines two equal and opposite forces into an action, so synthetic unity combines two equal and opposite dynamic communities into an event, thus establishing a mathematical analogy between action and event.
Keeping in mind that scientific knowledge must be tested and confirmed by experience and that its formulation must conform strictly with the laws of mathematics, let us turn our attention next to the bulwark of modern science, its physical mathematics.
It is generally recognized that the knowledge of the laws of motion lies at the root of all the different branches of science. This knowledge has been acquired from experimental methods with the aid of three dynamic factors, usually referred to as fundamental, and classically known as matter, space, and time. Matter (or force) is measured in units of weight, pounds or grams; space (or distance) is measured in units of length, feet or centimeters; and time (or period) is measured in seconds. These three measurements are recognized by physical science as elements and are referred to as "independent variables."
The measure of a complete performance is defined by the term work, w, and is determined by the product of weight, f, and the distance, d, through which the weight moves. W = fd. Hence work is expressed in foot pounds when the English system of measurement is used and in gram centimeters when expressed in terms of the metric system. It is only when we wish to know the rate at which the work is done that the introduction of the measurement time becomes necessary. For this purpose the term power, P, was introduced and defined as work divided by time. P = w/t. Hence power is derived from work by dividing either foot pounds or gram centimeters by seconds.
foot pounds/seconds or grams centimeters/seconds = Power.
In the above statement is presented one of the more elementary methods in what is generally known as physical mathematics, and it was with the aid of such methods that the laws of motion and the theories of classical mechanics were established. As these methods were universally accepted and the theories based upon such methods generally recognized by all the other branches of scientific research, it is to the pronouncements of physical science that we owe our present conception of, and attitude to, nature.
After many repeated assurances that the laws established by physical science were founded upon exact data, that they had been thoroughly tested and had never been found wanting, additional discoveries made it evident that such assurances could no longer be sustained. When finally the physicists themselves were prepared to admit this, they did so by informing the general public that the foundation of physical science was incorrect when applied to very large and very small scale phenomena. As the analytical methods pursued by science were not questioned, the only inference possible from such a statement was that the laws of nature vary according to size.
To account for this assumed difference, Einstein introduced his famous theory of relativity, by means of which it became possible to determine with mathematical accuracy the difference between so-called invariant and relative mass. While we shall have occasion to refer to this theory as we proceed, we may mention here that Einstein for purposes of confirmation applied his theory to the revolution of the planet Mercury. This enabled him to account for the 43 seconds of arc per century, which the old theory was unable to explain. This and other proofs provide us with additional evidence showing how the movements in nature can be described and measured with marvelous accuracy, but fail to bring us any nearer to a satisfactory understanding of the movements themselves. The particular value of this interesting and instructive theory as presented is the valuable service it rendered in calling attention to certain mistaken premises upon which Newtonian mechanics rested, and in paving the way for a new and more receptive attitude to nature by scientists in general. Incomplete as the theory so evidently is, it points out a distinct difference between a terrestrial mechanics based upon and applicable to the methods of man, and a celestial mechanics applicable to every movement produced by nature whether in solar or atomic systems. It should be noted however that this new theory does not supplant the older theories, but is gradually being superimposed upon them.
According to Einstein, nature is a four-dimensional space-time continuum in which no point has any fixed position. The theory recognizes that all physical objects are continually subject to change, that they exist as mere happenings at any given time and place, and hence are to be referred to as events. The theory of relativity assumes that in order to determine an event it must be coordinated by four numbers, derived from the three dimensions of space and the one dimension of time. On this basis Einstein introduced a mathematical technique in which there appears to be no more difference between length and time than between length and width and which, as such, differs widely from the mathematical methods of Newtonian physicists. It is these two kinds of applied physical mathematics that we shall try to consider in order to determine their relation respectively to nature on the one hand and to pure mathematics on the other.
* * * * * *
During the last century we were repeatedly told that the dynamic factors, matter, space, and time, were as old as mathematics itself and it was even suggested that mathematics was founded upon these factors. Whether work is done by man or by machine, by wind, water, earth, or fire, by electricity or chemical transformation, these factors have proved themselves a valuable guide. It is evident that man has obtained the knowledge of their use from nature, whose actions we recognize in physical movements and in physical growth and decay; and although we cannot readily measure growth or determine the actual unit value of these factors, they are nevertheless constantly revealed to us at the same time as they enter and play an important part in all our daily doings.
Because of their fundamental relation to physical science and also because scientists from time to time have expressed the opinion that all physical facts eventually can be expressed and explained with the aid of these factors, it would be reasonable to suppose that the question of their use in physical mathematics had been carefully considered, that the factors themselves, and their relation to each other and to nature, were thoroughly understood. Upon closer inquiry it becomes quite evident that this is not the case, but that the mathematical methods of physical science largely have been taken for granted. For no sooner do we begin to study these methods than some strikingly grotesque and apparently unexplainable features are brought to our attention. When viewed in the light of pure mathematics these methods distinctly violate one of its first elementary rules, and the question arises: How can pounds, feet, and seconds be multiplied and divided by one another, as previously indicated?
To make this question perfectly clear to every reader, let us introduce an elementary lesson in arithmetic. If one yard of cloth costs $2.00, what do ten yards cost? The answer is: 10 x $2.00, where apparently we multiplied yards by dollars. But the fact is that before we constructed the equation, we performed a lightning piece of calculation which, not being overstrenuous, usually is executed without the aid of a pencil, thus: 10 yards/1 yard = 10, that is we divide the ten yards by the one yard, relating to the $2.00, thereby canceling the yards and leaving the isolated number 10, by which we proceeded to multiply the $2.00. But in mathematical physics we are debarred from any such procedure and are obliged to allow each set of units to enter the equation as units of three distinctly different orders or quantities. How is this to be explained?
We turn to the many different treatises and textbooks on physics and try to learn how the physicists justify this mathematical method, only to find that each and all completely ignore the subject. We may learn everything else in these books, for they discuss, define, and explain elaborately almost every possible -- and sometimes impossible -- problem connected with mechanics, but nowhere do we find any direct reference to this particular question. Some of them tell us that "matter is that which can be acted upon, or can exert force," and thus distinctly define matter as a thing, and recognize that this thing, measured in pounds, is a factor in the product defined as work. But as to how pounds can be multiplied by feet and divided by seconds, there seems to reign complete and absolute silence. We begin to wonder whether the answer is really so self-evident as to justify us in taking it for granted!
It seems, however, that this question was once for all disposed of on the general supposition that the number of dimensions in a manifold depends upon what is necessary for the determination of its complexity, and that the physicist abstracts dimensions just as the geometrician abstracts the dimensions of form. But unless a clearly defined mathematical rule for such abstraction can be established, such general explanations are entirely unsatisfactory, as was made evident when the relativists added a fourth dimension to space.
In the effort to discover something that can guide us to a satisfactory answer to our query, let us turn our attention to the classical geometric dimensions of form, where once more we are facing an apparent anomaly; for in determining the contents of form, we seem to be multiplying homogeneous units, inches, an equally impossible mathematical proposition. Pure mathematics insists that before we can enter a measurement as a factor in a product, it must be completely abstracted from its subject of reference, in other words it must be reduced to an isolated number. Let us therefore examine this geometric method and try to learn something about abstractions from geometry itself.
When we measure the length, width, and thickness of a body and multiply them we obtain the measurement of the complete volume or quantity of the body. When calculating the volume of an irregular form, it may be necessary first to divide this form into infinitesimal parts, but this indirect method represents means to the same end. Let us try to determine mathematically what each of the dimensions in a geometric quantity actually represents. The way of resolving a product into its various elements is by dividing it by one or more of these elements. So if we wish to know what length is, we must divide the complete product by the other factors, thus:
Length x width x thickness/width x thickness = length x 1w x 1t
This gives us the mathematical definition of abstracted length and demonstrates something which we have known all the time namely, that the length of a body does not exist by itself but by virtue of its companions, width and thickness. Length, width, and thickness are three magnitudes constituting a sort of indissoluble partnership. Sometimes one partner and sometimes another may be said to assert itself more than the others, or any one of them may retire from visible participation, but never altogether. For none of the partners can completely sever its connection, none of them can ever become less than a silent partner, however infinitesimal may be the dimensional value or influence in this partnership. If one of the partners could withdraw completely, its unit-value would be zero, and the mathematical result would wipe all the partners out of existence. We cannot logically consider or define the length of a quantity without including the partners that determine length, for without such determination, length is a meaningless and empty word.
When we measure length with a yardstick, we determine one of the inseparable dimensional aspects of the body with the aid of its other aspects. When we enter this measurement as a factor in an equation in which the other factors have been similarly introduced, what was a definite dimension has now become a factorial magnitude, a numerical relativity, while the complete product becomes the measure of a geometric quantity.
In order to understand this we must draw a clear distinction between magnitudes and dimensions. Magnitudes are continuous, while dimensions are discontinuous. In order to distinguish magnitudes we adopt standard measurements dimensions just as we adopt names with which to distinguish objects. But objects are not names any more than magnitudes are dimensions. If magnitudes were dimensions, we should be multiplying definite conceptions by each other, or inches by inches. It follows that before we can multiply numbers belonging to dimensions, we must be able to abstract the defining dimensional aspects from these numbers, and that this can be done only when a condition exists for transforming dimensions into numerical relativities.
That such a condition exists in this geometric equation is confirmed by experience which shows that length, width, and thickness have no independent existence and that when any one of these dimensions is referred to separately, it must inferentially include its partners in order to make them objects of thought. Hence mathematics informs us that dimensions can only be applied to factors in a product, when the product represents a community of inseparable and interdefining dimensions of a quantity.
* * * * * *
Before leaving geometry let us examine a point, which our school books tell us is a "location without parts," and it is upon such a point, expressed mathematical as 0l x 0w x 0t that the science of geometry is supposed to have been established. Once more we apply the resolving process in order to determine what a mathematical point is. By dividing out the numerical values of all the factors in the way already described, we learn that the mathematical point is 1l x 1w x 1t. In other words a point is a quantity whose magnitudes are silent or latent. We may make the unit value of these silent magnitudes as small as we like -- billions of times smaller than an electron -- but not zero. When zero is reached the mathematical process ceases.
From the foregoing we have learned that length, width, and thickness represent three inseparable and interdefining magnitudes, capable of expressing an infinite range of numerical relativities and of determining the geometric quantity of all extensions from points to universes.
Is this interpretation correct? Kant insisted that "a mathematical demonstration carries necessity on its face" and this necessity appears obvious. Recently, however, there has been a tendency to question Euclidean geometry, and we have been informed by eminent mathematicians that geometry cannot demonstrate the truth of its own theorems. Be this as it may, the above demonstration indicates that what geometry cannot do for itself some very elementary arithmetic can do for geometry. For just as the arithmetically established partners unite the geometric magnitudes in any given quantity, so do they bind pure mathematics to objects of experience.